Bạn đang tìm kiếm công thức tính đường chéo hình thoi? Hình thoi hay bất kỳ một hình học nào khác đều có những công thức tính của riêng nó, ngoài tính diện tích hình thoi, tính chu vi hình thoi là những dạng bài toán thường gặp thì tính đường chéo hình thoi cũng là một dạng toán hay và gặp thường xuyên khi học toán hình. Mời bạn cùng Trường Hải Tiến Giang tìm hiểu công thức tính đường chéo hình thoi & ví dụ minh họa trong bài viết dưới đây nhé.
I. Hình thoi là gì? Đường chéo hình thoi là gì?
Hình thoi trong hình học Euclide là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.
Tính chất hình thoi
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác các góc của hình thoi
- Hình thoi có tất cả các tính chất của hình bình hành (có cạnh đối song song và bằng nhau; có các góc đối bằng nhau; hai đường chéo cắt nhau tại trung điểm mỗi đường)

Đường chéo của hình thoi là đường nối hai đỉnh đối diện của hình thoi, đường chéo chia hình thoi thành hai tam giác đều với các cạnh bằng nhau. Hình thoi có hai đường chéo, và chúng cắt nhau tại trung điểm của hình thoi.
II. Công thức tính đường chéo hình thoi
1. Công thức tính đường chéo hình thoi theo công thức tính diện tích hình thoi
dùng công thức tính diện tích hình thoi là: \(S=\frac{d_1 \times d_2}{2}\)
Trong đó: S là diện tích hình thoi; \(\mathrm{d}_1 \text { và } \mathrm{d}_2\) là hai đường chéo của hình thoi.
Từ đó ta có công thức tính đường chéo hình thoi là \(d_1=\frac{S \times 2}{d_2}\) hay \(d_2=\frac{S \times 2}{d_1}\)

2. Công thức tính đường chéo hình thoi dựa vào định lý cosin
Định lý cosin biểu diễn sự liên quan giữa chiều dài của các cạnh của một tam giác với cosin của góc tương ứng.
Công thức cosin: \(c^2=a^2+b^2+2 a b \cos \gamma\)
Trong đó: a, b, c là các cạnh của tam giác, y là góc tương ứng giữa hai cạnh a và b.

3. Công thức tính đường chéo hình thoi theo định lý Pytago
Áp dụng định lý Pytago cho tam giác vuông với góc vuông là giao điểm của hai đường chéo hình thoi. Bình phương cạnh huyền sẽ bằng tổng bình phương hai cạnh còn lại.

Ví dụ 1: Cho hình thoi ABCD có cạnh a và một góc ABC = 60 độ. Tính hai đường chéo hình thoi.
Bài giải
Vì hình thoi có các cạnh bằng nhau, nên hình thoi ABCD có các cạnh đều bằng a.
Xét tam giác ABCD có: AB = BC = a
Góc ABC = 60 độ.
=> Tam giác ABC là tam giác đều cạnh a.
Vậy AB = AC = BC = a. Độ dài đường chéo chính AC = a.
Gọi I là giao điểm của hai đường chéo, áp dụng định lý Pytago cho tam giác vuông ABI ta có:
\(B I^2=A B^2-A I^2=a^2-\left(\frac{a}{2}\right)^2=a^2\left(1-\frac{1}{4}\right)=\frac{3}{4} a^2\)
=> \(B I=\frac{a \sqrt{3}}{2}\)
Vậy đường chéo BD = BI x 2 = \(a \sqrt{3}\)
III. Ví dụ minh họa
Dạng 1: Bài toán cho biết độ dài 1 đường chéo và yêu cầu học sinh tìm độ dài đường chéo còn lại
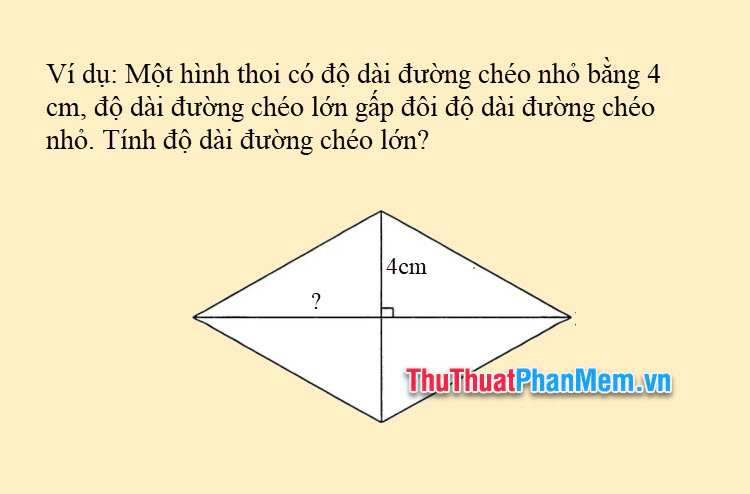
Ví dụ 2: Một hình thoi có độ dài đường chéo nhỏ bằng 4 cm, độ dài đường chéo lớn gấp đôi độ dài đường chéo nhỏ. Tính độ dài đường chéo lớn?
Bài giải
Gọi đường chéo nhỏ, lớn của hình thoi lần lượt là \(\mathrm{d}_1\) và \(\mathrm{d}_2\).
Ta có: \(\mathrm{d}_1\) = 4cm và \(\mathrm{d}_2\) gấp đôi \(\mathrm{d}_1\).
Vậy độ dài đường chéo lớn \(\mathrm{d}_2\) = 4 x 2 = 8 cm.
Ví dụ 3: Một hình thoi có hiệu độ dài hai đường chéo là 10 cm, đường chéo thứ nhất gấp 3 lần đường chéo thứ hai. Tính độ dài hai đường chéo?
Bài giải
Gọi đường chéo lớn, nhỏ của hình thoi lần lượt là \(\mathrm{d}_1\) và \(\mathrm{d}_2\)
b. \(\mathrm{d}_1\) – \(\mathrm{d}_2\) = 10cm, \(\mathrm{d}_1\) = 3\(\mathrm{d}_2\)
Suy ra: 3\(\mathrm{d}_2\) – \(\mathrm{d}_2\) = 10 nên \(\mathrm{d}_2\) = 5cm, \(\mathrm{d}_1\) = 15cm.
Dạng 2: Bài toán cho biết diện tích và độ dài 1 đường chéo
Với bài toán này bạn chỉ cần áp dụng công thức tính đường chéo hình thoi theo diện tích hình thoi ở trên là có thể giải được.
Ví dụ 4: Cho một hình thoi có diện tích là 200 cm vuông, độ dài 1 đường chéo là 10. Tính độ dài đường chéo còn lại.

Bài giải:
Áp dụng công thức tính đường chéo hình thoi theo diện tích hình thoi \(d 1=\frac{s \times 2}{d 2}\) ta có:
Đường chéo còn lại là: (200 x 2) : 10 = 40 cm.
Vậy đường chéo còn lại của hình thoi dài 40 cm.
Dạng 3: Bài toán cho biết cạnh và đường cao của hình thoi, yêu cầu học sinh tìm độ dài hai đường chéo
Ví dụ 5: Cho hình thoi ABCD có cạnh bằng 12,5cm, đường cao bằng 6,72 cm và AC nhỏ hơn BD. Hỏi độ dài hai đường chéo AC và BD lần lượt bằng bao nhiêu?
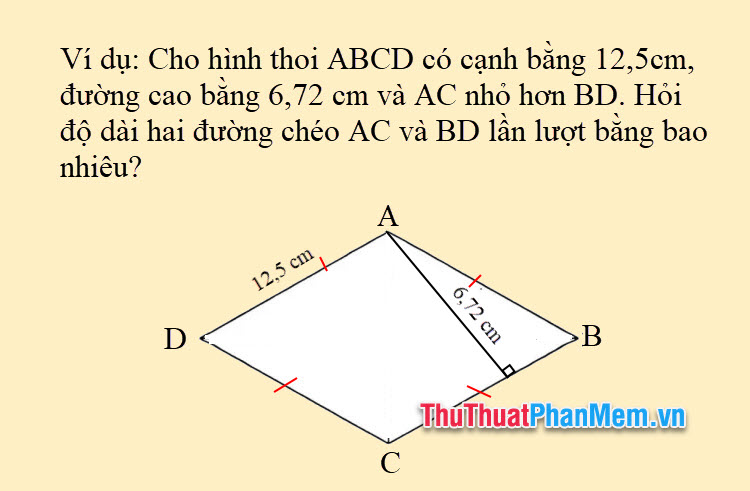
Bài giải
Áp dụng công thức tính diện tích hình thoi: S = h x a = 6,72 x 12,5 = 84cm².
\(=>\frac{AC \times BD}{2}\) = 84 => 2AC x BD = 336
Gọi O là giao điểm của hai đường chéo hình thoi.
Xét tam giác vuông AOB, ta có \(A B^2=O A^2+O B^2\)
mà \(O A=\frac{1}{2} A C ; O B=\frac{1}{2} B D=> 12,5^2 =\frac{\left (A C^2+B D^2)\right.}{4}<=>625=A C^2+B D^2\)
=> AC + BD = 31 (1).
AC² + BD² = 625 <=> AC² + BD² – AC x AB = 625 – 336 <=> (BD – AC)² = 289
=> BD – AC = 17 (Theo đề bài BD > AC) (2)
Từ (1) và (2), ta có: BD = 24, AC = 7cm.
Trên đây Trường Hải Tiến Giang đã chia sẻ với bạn các khái niệm cơ bản về hình thoi, công thức tính đường chéo hình thoi theo diện tích, công thức tính đường chéo hình thoi theo định lý cosin, công thức tính đường chéo hình thoi theo định lý Pytago và ví dụ minh họa cụ thể. Hi vọng sau khi tham khảo bài viết này bạn sẽ hiểu rõ hơn về cách tính đường chéo hình thoi và có thể dễ dàng giải những bài tập tính đường chéo hình thoi. Cảm ơn bạn đã quan tâm và theo dõi bài viết này.
Bạn đang tìm kiếm công thức tính đường chéo hình thoi? Hình thoi hay bất kỳ một hình học nào khác đều có những công thức tính của riêng nó, ngoài tính diện tích hình thoi, tính chu vi hình thoi là những dạng bài toán thường gặp thì tính đường chéo hình thoi cũng là một dạng toán hay và gặp thường xuyên khi học toán hình. Mời bạn cùng Trường Hải Tiến Giang tìm hiểu công thức tính đường chéo hình thoi & ví dụ minh họa trong bài viết dưới đây nhé.
