Để giúp bổ sung lại những kiến thức còn thiếu, những kiến thức mà bạn chưa hiểu về hình chóp, các công thức tính diện tích hình chóp. Bài viết dưới đây Trường Hải Tiến Giang chia sẻ với bạn các công thức tính diện tích hình chóp & ví dụ minh họa, mời bạn cùng tham khảo nhé.
I. Hình chóp là gì? Hình chóp đều là gì?
1. Hình chóp là gì?
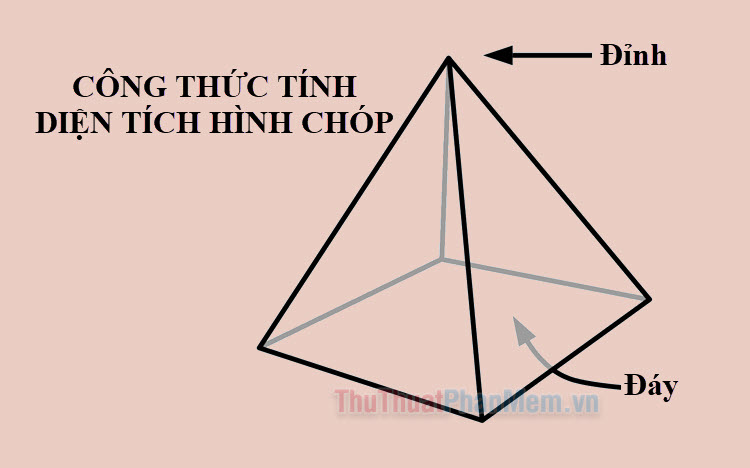
Trong hình học không gian, hình chóp là một khối đa diện có đáy là một đa giác lồi, các mặt bên đều là hình tam giác và có chung một đỉnh, đây chính là đỉnh của hình chóp. Đỉnh của hình chóp không nằm trên mặt đáy.
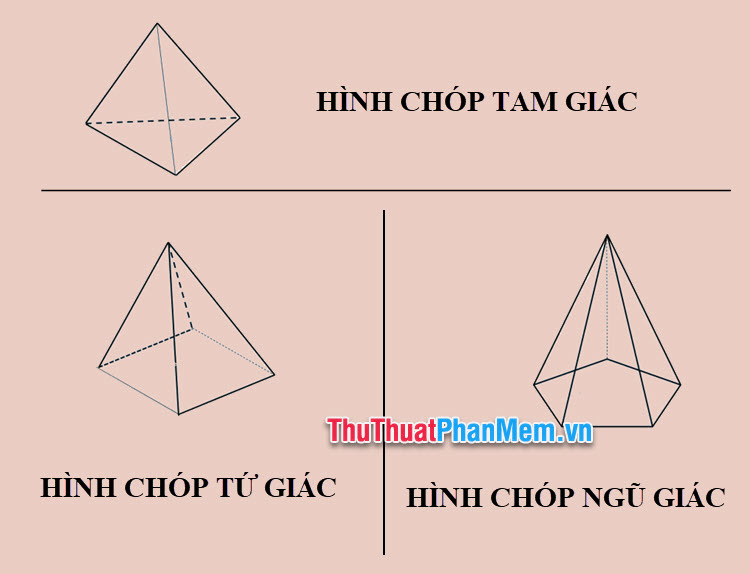
Có rất nhiều loại hình chóp khác nhau, tên của hình chóp sẽ được gọi dựa theo hình đáy của chúng. Ví dụ: Hình chóp tam giác đều là hình chóp có đáy là hình tam giác đều, hình chóp tam giác là hình chóp có đáy là hình tam giác, hình chóp tứ giác là hình chóp có đáy là hình tứ giác, hình chóp hình thang là hình chóp có đáy là hình thang, hình chóp hình bình hành là hình chóp có đáy là hình bình hành,…
2. Tính chất của hình chóp
- Đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp
- Hình chóp có cạnh bên hợp với mặt đáy các góc bằng nhau hoặc các cạnh bên bằng nhau thì chân đường cao chính là tâm đường tròn ngoại tiếp đáy
- Hình chóp có mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy thì đường cao của hình chóp sẽ là đường cao của mặt bên hoặc mặt chéo đó
- Hình chóp có các mặt bên hợp với mặt đáy các góc bằng nhau hoặc có các đường cao của các mặt bên xuất phát từ 1 đỉnh bằng nhau thì chân đường cao là tâm đường tròn nội tiếp mặt đáy
3. Hình chóp đều là gì?
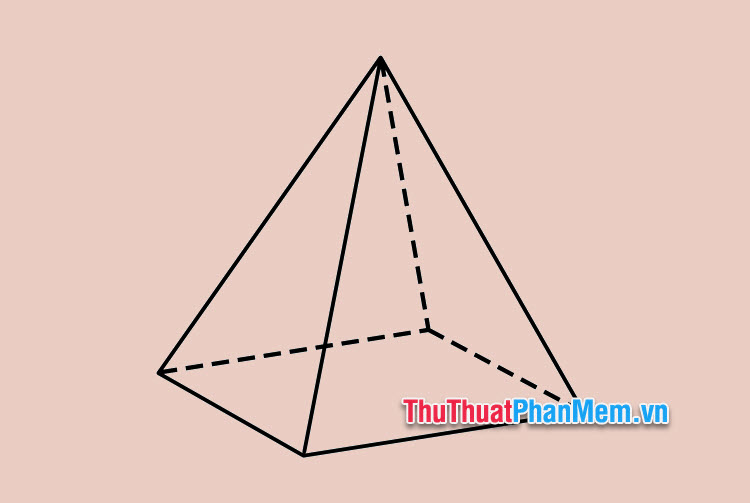
Trong hình học không gian, hình chóp đa giác đều là dạng hình chóp đặc biệt thường gặp, hình chóp này có đáy là các đa giác đều với các mặt bên là các tam giác bằng nhau. Ví dụ: Hình chóp tam giác đều, hình chóp tứ giác đều,…
Tính chất hình chóp đều:
- Đáy của hình chóp đều là các đa giác đều ví dụ như: Hình vuông, hình tam giác đều, hình ngũ giác đều,…
- Tâm của đa giác đáy trùng với chân đường cao của hình chóp đều
II. Công thức tính diện tích hình chóp
1. Công thức tính diện tích xung quanh hình chóp
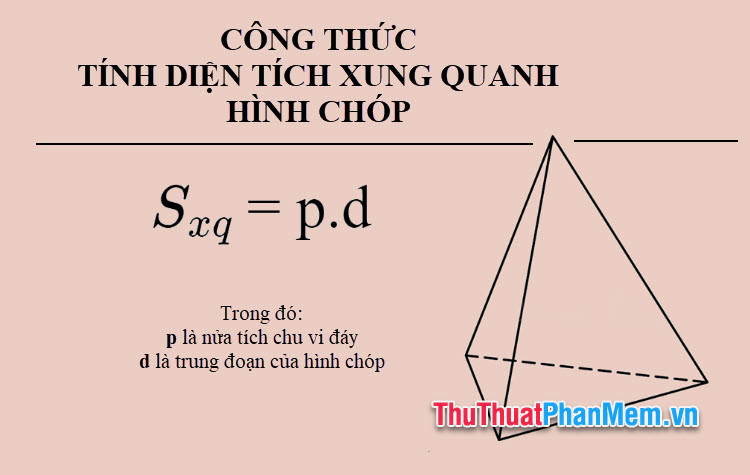
Diện tích xung quanh của hình chóp là tổng diện tích các mặt bên của hình chóp. Để tính diện tích xung quanh, ta dùng công thức:
\(S_{x q}\) = p.d
Trong đó:
- \(S_{x q}\) là diện tích xung quanh của hình chóp
- p là nửa tích chu vi đáy
- d là trung đoạn của hình chóp (đường cao vẽ từ đỉnh hình chóp xuống trung điểm của mỗi cạnh đa giác đáy đều là trung đoạn của hình chóp đó)
Lưu ý: Công thức trên chỉ áp dụng cho các hình chóp có các mặt bên là hình tam giác đều. Nếu hình chóp có các mặt bên khác nhau, ta cần tính diện tích riêng cho từng mặt bên và cộng tổng lại để tính diện tích xung quanh.
2. Công thức tính diện tích toàn phần hình chóp
Diện tích toàn phần của hình chóp là tổng diện tích xung quanh hình chóp và diện tích đáy hình chóp đó.
\(S_{t p}\) = \(S_{x q}\) + \(S_{đ á y}\)
III. Ví dụ minh họa
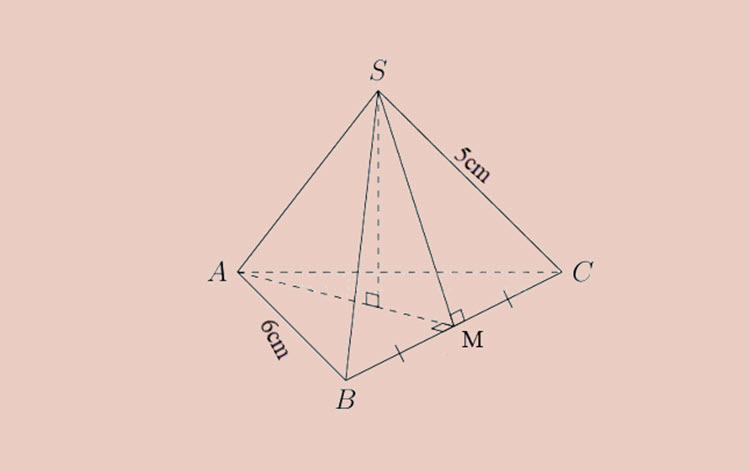
Ví dụ 1: Cho hình chóp tam giác đều có cạnh đáy dài 6 cm, độ dài các cạnh bên là 5cm. Tính diện tích xung quanh và diện tích toàn phần.
Bài giải
– Bài toán cho hình chóp tam giác đều có cạnh đáy dài 6cm vậy các cạnh của tam giác đáy đều bằng 6 cm, chiều dài các cạnh bên hình chóp là 5cm.
– Gọi hình chóp tam giác đều là S.ABC, đỉnh S vẽ đường thẳng nối với trung điểm của đoạn AC đặt là M như hình vẽ, đây chính là trung đoạn d của hình chóp tam giác đều S.ABC.
– Vì tam giác SBC là tam giác cân tại S nên tam giác SBM là tam giác vuông tại M, BM bằng 1 nửa BC và bằng 3 cm, áp dụng định lý Pytago cho tam giác vuông SBM, ta có:
\(S M^2=S B^2-B M^2=5^2-3^2=16\)
=> SM = 4 cm (SM chính là trung đoạn d của hình chóp).
– Áp dụng công thức tính diện tích xung quanh hình chóp, ta có:
\(S_{x q}=p \cdot d=\frac{6 \times 3}{2} \cdot 4=9.4=36 \mathrm{~cm}^2\)
– Diện tích tam giác đáy bằng: \(S_{\text {đáy }}=a^2 \times \frac{\sqrt{3}}{4}=6^2 \times \frac{\sqrt{3}}{4}=9 \sqrt{3} \mathrm{~cm}^2\)
– Áp dụng công thức tính diện tích toàn phần hình chóp, ta có:
\(S_{t p}=S_{x q}+S_{\mathrm{d}}=36+9 \sqrt{3} \approx 51,59 \mathrm{~cm}^2\)
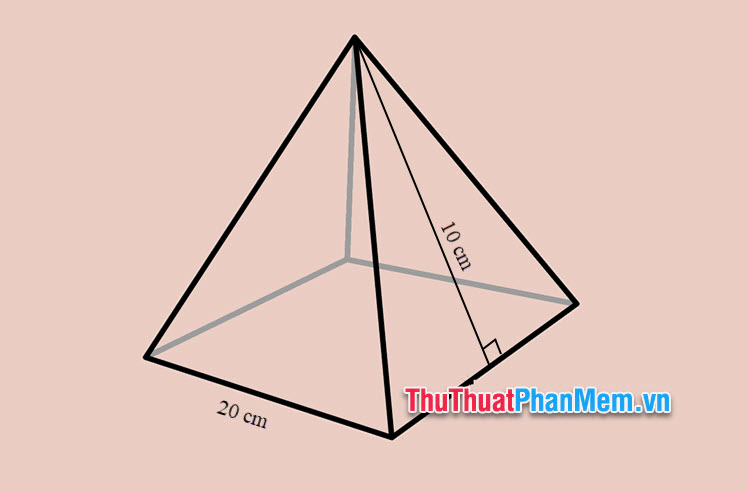
Ví dụ 2: Cho hình chóp tứ giác đều có chiều cao tam giác mỗi mặt bên bằng 10 cm, độ dài cạnh đáy bằng 20 cm. Tính diện tích toàn phần hình chóp tứ giác đều.
Bài giải
Vì là hình chóp tứ giác đều nên các cạnh của tứ giác đáy đều bằng 20 cm.
Diện tích mặt bên (hình tam giác) của hình chóp là:
\(S=\frac{1}{2} \times 10 \times 20=100 \mathrm{~cm}^2\)
Vậy diện tích xung quanh hình chóp là:
\(S_{x q}=4 \times 100=400 \mathrm{~cm}^2\)
Áp dụng công thức tính diện tích toàn phần hình chóp, ta có:
\(S_{t p}=S_{x q}+S_{\mathrm{a}}=400+20.20=800 \mathrm{~cm}^2\)
Vậy diện tích toàn phần của hình chóp trên là \(800 \mathrm{~cm}^2\).
Như vậy, Trường Hải Tiến Giang đã chia sẻ với bạn công thức tính diện tích hình chóp, công thức tính diện tích xung quanh, công thức tính diện tích toàn phần và ví dụ minh họa. Hi vọng với những kiến thức hữu ích về hình chóp này, bạn sẽ nắm rõ kiến thức hơn để có thể dễ dàng giải quyết các bài toán tính diện tích hình chóp. Cảm ơn bạn đã quan tâm và theo dõi bài viết này.
Để giúp bổ sung lại những kiến thức còn thiếu, những kiến thức mà bạn chưa hiểu về hình chóp, các công thức tính diện tích hình chóp. Bài viết dưới đây Trường Hải Tiến Giang chia sẻ với bạn các công thức tính diện tích hình chóp & ví dụ minh họa, mời bạn cùng tham khảo nhé.
