Nếu bạn chưa nắm chắc kiến thức về khối lập phương, vậy mời bạn cùng Trường Hải Tiến Giang tìm hiểu về khối lập phương, công thức diện tích khối lập phương & ví dụ minh họa trong bài viết dưới đây nhé.
I. Khối lập phương là gì?
Khối lập phương là hình khối có chiều rộng, chiều dài, chiều cao đều có độ dài bằng nhau. Có 6 mặt đều là hình vuông bằng nhau. Hay khối lập phương chính là hình hộp chữ nhật có tất cả các cạnh bằng nhau.

Tính chất của khối lập phương
- Khối lập phương có 8 mặt phẳng đối xứng
- Khối lập phương có 12 cạnh bằng nhau, 8 đỉnh, cứ 3 cạnh gặp nhau tại 1 đỉnh
- Đường chéo của hình khối lập phương dài bằng nhau
- Khối lập phương có 4 đường chéo cắt nhau tại một điểm, đó được xem là tâm đối xứng của khối lập phương
II. Công thức tính diện tích khối lập phương
Cho khối lập phương
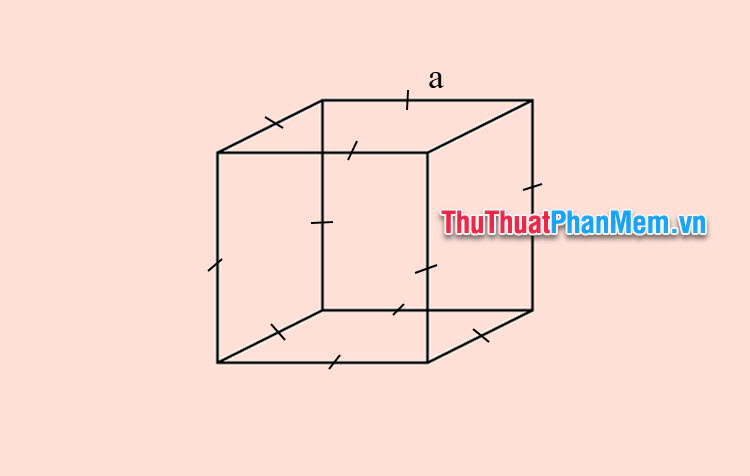
Một số quy ước:
- a: Độ dài của cạnh lập phương
- P: Chu vi khối lập phương
- \(\mathrm{S}_{\mathrm{bm}}\): Diện tích bề mặt khối lập phương
- \(\mathrm{S}_{\mathrm{xq}}\): Diện tích xung quanh khối lập phương
- \(\mathrm{S}_{\mathrm{tp}}\): Diện tích toàn phần khối lập phương
- V: thể tích
1. Công thức tính diện tích xung quanh khối lập phương
Công thức tính diện tích xung quanh khối lập phương là:
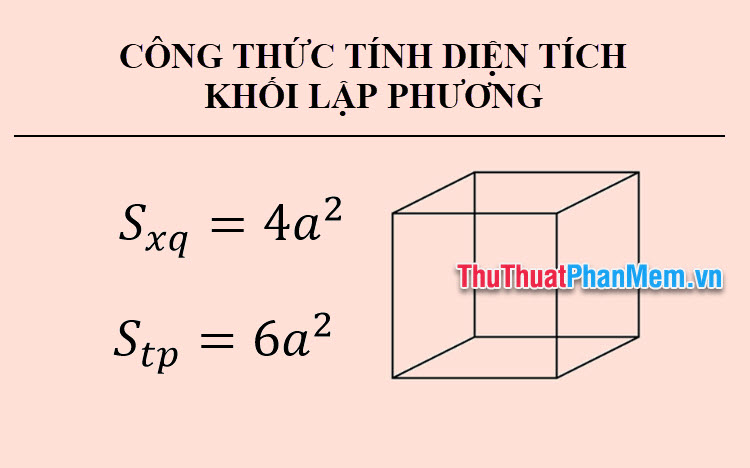
\( S_{x q}=4 a^2 \)
2. Công thức tính diện tích toàn phần khối lập phương
Công thức tính diện tích toàn phần khối lập phương là:
\( S_{t p}=6 a^2 \)
3. Phát biểu bằng lời
– Diện tích xung quanh khối lập phương bằng bình phương độ dài một cạnh nhân với 4.
– Diện tích toàn phần khối lập phương bằng bình phương độ dài một cạnh nhân với 6.
– Diện tích xung quanh chỉ tính các mặt phẳng nằm ở bên ngoài khối lập phương, còn diện tích toàn phần bao gồm cả diện tích các mặt phẳng nằm ở bên trong khối lập phương.
III. Các dạng bài tập tính diện tích xung quanh và toàn phần khối lập phương
Một số dạng bài tập tính diện tích xung quanh hoặc tính diện tích toàn phần khối lập phương thường gặp.
1. Biết cạnh khối lập phương, tính diện tích khối lập phương
Dạng bài tập này đề bài sẽ cho biết cạnh của khối lập phương, yêu cầu tính diện tích xung quanh hoặc diện tích toàn phần của khối lập phương.
Cách giải: Bạn chỉ cần áp dụng công thức tính diện tích xung quanh hoặc diện tích toàn phần của khối lập phương để giải.

2. Biết diện tích của khối lập phương, tìm diện tích một mặt
Đề bài sẽ cho biết diện tích xung quanh hoặc diện tích toàn phần của khối lập phương, yêu cầu tìm diện tích một mặt của khối lập phương.
Cách giải: Bạn chỉ cần nhớ cách tính diện tích một mặt theo diện tích xung quanh hay diện tích toàn phần là có thể dễ dàng giải được dạng toán này.
- Diện tích một mặt của khối lập phương = Diện tích xung quanh : 4
- Diện tích một mặt của khối lập phương = Diện tích toàn phần : 6
3. Biết diện tích của khối lập phương, tìm độ dài cạnh của khối lập phương.
Bài tập cho biết diện tích xung quanh hoặc diện tích toàn phần của khối lập phương, yêu cầu tìm độ dài cạnh của khối lập phương.
Cách giải: Đầu tiên bạn tính diện tích một mặt của khối lập phương dựa vào diện tích xung quanh hoặc diện tích toàn phần.
Diện tích một mặt chính là diện tích hình vuông, bạn lập luận để tìm ra độ dài cạnh từ diện tích hình vuông đó.
IV. Ví dụ minh họa tính diện tích khối lập phương
Ví dụ 1: Tính diện tích xung quanh và diện tích toàn phần của khối lập phương có cạnh dài 6cm.
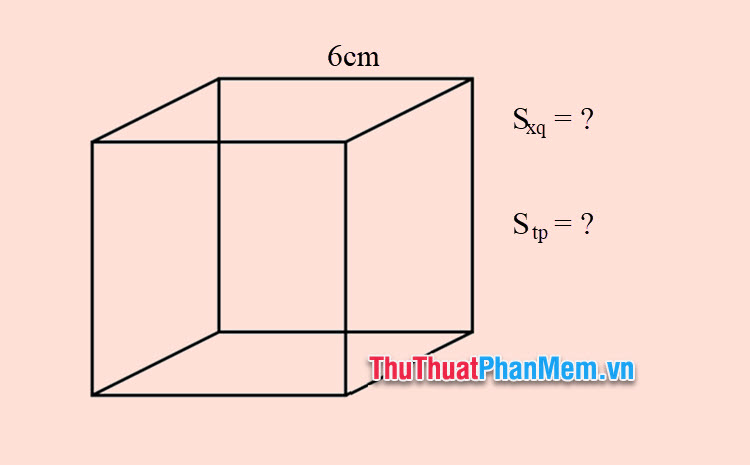
Bài giải
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần ta có:
\(S_{x q}=4 \cdot a^2=4 \cdot 6^2=144\)
\(S_{t p}=6 \cdot a^2=6 \cdot 6^2=216\)
Vậy diện tích xung quanh khối lập phương là 144 \(\mathrm{cm}^2\).
Diện tích toàn phần khối lập phương là 216 \(\mathrm{cm}^2\)
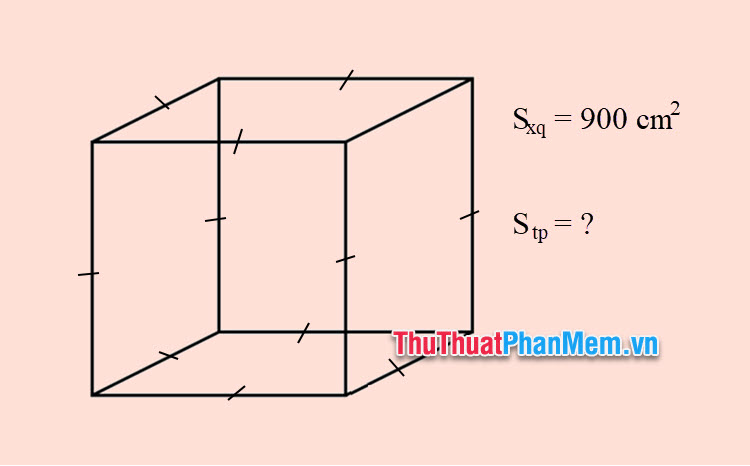
Ví dụ 2: Cho một khối lập phương có diện tích xung quanh bằng 900 \(\mathrm{cm}^2\). Tính diện tích toàn phần khối lập phương.
Bài giải
Áp dụng công thức tính diện tích xung quanh \( S_{x q}=4 a^2 \), ta có:
\(a=\sqrt{\frac{S_{x q}}{4}}=\sqrt{\frac{900}{4}}=\sqrt{225}=15 \mathrm{~cm}\)
Áp dụng công thức tính diện tích toàn phần \( S_{t p}=6 a^2 \), ta có:
\(S_{t p}=6 . a^2=6.15^2=1350 \mathrm{~cm}^2\)
Vậy diện tích toàn phần khối lập phương là \(1350 \mathrm{~cm}^2\)
Như vậy, bạn đã vừa cùng Trường Hải Tiến Giang tìm hiểu về khối lập phương cũng như công thức diện tích khối lập phương & ví dụ minh họa cụ thể. Hi vọng với những kiến thức mà bài viết chia sẻ ở trên, sẽ góp thêm một phần kiến thức về khối lập phương để giúp bạn giải những bài toán về tính diện tích khối lập phương. Cảm ơn bạn đã quan tâm và theo dõi bài viết này.
Nếu bạn chưa nắm chắc kiến thức về khối lập phương, vậy mời bạn cùng Trường Hải Tiến Giang tìm hiểu về khối lập phương, công thức diện tích khối lập phương & ví dụ minh họa trong bài viết dưới đây nhé.