Bài tập các trường hợp đồng dạng của tam giác giúp các em học sinh làm quen với các dạng bài hay gặp trong các bài thi học sinh giỏi với các câu hỏi khó giành điểm 9 – 10 và có chiến lược thời gian làm bài thi phù hợp nhất.
Các trường hợp đồng dạng của tam giác mà Trường Hải Tiến Giang giới thiệu bao gồm tóm tắt kiến thức lý thuyết, ví dụ minh họa kèm theo các dạng bài tập tự luyện trọng tâm. Qua đó giúp các em học sinh rèn luyện tư duy, hệ thống kiến thức bao quát những dạng toán thường gặp. Bên cạnh đó các bạn xem thêm bài tập về Bình phương của một tổng, bài tập hiệu hai bình phương.
I. Lý thuyết tam giác đồng dạng cần ghi nhớ
1. Định lý Ta – lét trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
2. Định lý đảo và hệ quả của định lý Ta – let
a) Định lý Ta – lét đảo.
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
b) Hệ quả của định lý Ta – let.
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
3. Tính chất đường phân giác trong tam giác
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của đoạn ấy.
Tam giác cân có hai đường phân giác. Để chứng minh điều này, ta lấy tam giác ABC cân và kí hiệu O là giao điểm của hai đường phân giác. Ta cần chứng minh rằng đường thẳng OA và OB là hai đường phân giác.
- Bước 1: Ta có tam giác ABC cân, nên AB=AC.
- Bước 2: Vì O là giao điểm của hai đường phân giác, nên tam giác AOB và AOC là tam giác đồng quy tại O.
- Bước 3: Do tam giác đồng quy có điểm đồng quy nằm trên đường thẳng nối các điểm đồng quy, nên tam giác ABC có đường thẳng OA là đường phân giác.
Tương tự, ta chứng minh được rằng đường thẳng OB cũng là đường phân giác của tam giác ABC.
Vậy, tam giác cân có hai đường phân giác.
4. Tam giác đồng dạng
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
Các góc: A’ = A; B’ = B; C’ = C;
Tỉ lệ các cạnh: A’B/AB = B’C’/BC = C’A’/CA
– Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
5. Ba trường hợp đồng dạng của tam giác
a) Trường hợp thứ nhất (c.c.c)
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Trường hợp thứ hai (c.g.c)
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.
c) Trường hợp thứ ba (g.g.g)
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
6. Các trường hợp đồng dạng của tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu :
– Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
– Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
II. Ví dụ về các trường hợp đồng dạng của tam giác
Ví dụ 1: Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
Lời giải:
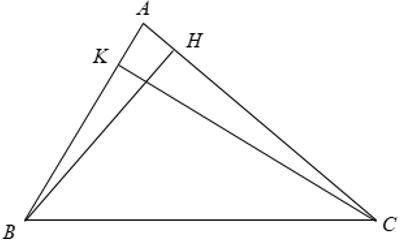
Xét Δ ABH và Δ ACK có 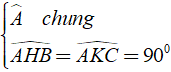
⇒ Δ ABH ∼ Δ ACK ( g – g )
Ví dụ 2:
Cho Δ ABC,Δ A’B’C’ có độ dài các cạnh như hình vẽ. Chứng minh Δ ABC ∼ Δ A’B’C’
Lời giải:
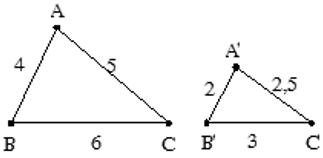
Xét Δ ABC,Δ A’B’C’ có A’B’/AB = A’C’/AC = B’C’/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A’B’C’ ( c – c – c )
III. Bài tập các trường hợp đồng dạng của tam giác
Bài 1: Cho tam giác vuông ABC (Â = 900) có AB = 9cm, AC = 12cm. Tia phân giác góc A cắt BC tại D. Từ D kẻ DE vuông góc với AC (E thuộc AC) .
a) Tính độ dài các đoạn thẳng BD, CD và DE.
b) Tính diện tích các tam giác ABD và ACD.
Bài 2: Cho hình thang ABCD (AB //CD). Biết AB = 2,5cm; AD = 3,5cm; BD = 5cm; và góc DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh BC và CD.
Bài 3: Cho tam giác ABC vuông tại A, AB =15 cm; AC = 20 cm . Kẻ đường cao AH
a/ Chứng minh: ΔABC đồng dạng ΔHBA từ đó suy ra: AB2 = BC. BH
b/ Tính BH và CH.
Bài 4: Cho tam giác ABC vuông tai A, đường cao AH ,biết AB = 15 cm, AH = 12cm
a/ CM: ΔAHB đồng dạng ΔCHA
b/ Tính các đoạn BH, CH, AC
Bài 5: Cho hình bình hành ABCD, trên tia đối của tia DA lấy DM = AB, trên tia đối của tia BA lấy BN = AD. Chứng minh:
a) ΔCBN và ΔCDM cân.
b) ΔCBN đồng dạng ΔMDC
c) Chứng minh M, C, N thẳng hàng.
Bài 6: Cho tam giác ABC (AB < AC), hai đường cao BE và CF gặp nhau tại H, các đường thẳng kẻ từ B song song với CF và từ C song song với BE gặp nhau tại D. Chứng minh
a) ΔABE đồng dạng ΔACF
b) AE . CB = AB . EF
c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng.
Bài 7: Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
a) CMR: AE . AC = AF . AB
b) CMR: ΔAFE đồng dạng ΔACB
c) CMR: ΔFHE đồng dạng ΔBHC
d ) CMR: BF . BA + CE . CA = BC2
Bài 8: Cho hình thang cân MNPQ (MN // PQ, MN < PQ), NP = 15 cm, đường cao NI = 12 cm, QI = 16 cm
a) Tính độ dài IP, MN
b) Chứng minh rằng: QN ⊥ NP
c) Tính diện tích hình thang MNPQ
d) Gọi E là trung điểm của PQ. Đường thẳng vuông góc với EN tại N cắt đường thẳng PQ tại K. Chứng minh rằng : KN 2 = KP. KQ
Bài 9: Cho hình bình hành ABCD , trên tia đối của tia DA lấy DM = AB, trên tia đối của tia BA lấy BN = AD. Chứng minh :
d) ΔCBN và ΔCDM cân.
e) ΔCBN đồng dạng ΔMDC
f) Chứng minh M, C, N thẳng hàng.
Bài 10: Cho tam giác ABC (AB < AC), hai đường cao BE và CF gặp nhau tại H, các đường thẳng kẻ từ B song song với CF và từ C song song với BE gặp nhau tại D. Chứng minh
a) ΔABE đồng dạng ΔACF
b) AE . CB = AB . EF
c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng.
Bài 11: Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
a) CMR : AE . AC = AF . AB
b) CMR AFE ACB
c) CMR: FHE BHC
d ) CMR : BF . BA + CE . CA = BC2
Bài 12 : Cho tam giác ABC cân tại A và M là trung điểm của BC. Lấy các điểm D,E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME bằng góc B.
a) Chứng minh BDM đồng dạng với CME
b) Chứng minh BD.CE không đổi.
c) Chứng minh DM là phân giác của góc BDE
Bài 13 Cho tam giác ABC vuông tại A , có AB = 6cm ; AC = 8cm. Vẽ đường cao AH (H ∈ BC)
a) Tính độ dài cạnh BC .
b) Chứng minh tam giác HBA đồng dạng với tam giác ABC
c) Vẽ phân giác AD của góc A (D ∈ BC) . Chứng minh rằng điểm H nằm giữa hai điểm B và D .
Câu 14: Cho tam giác ABC vuông tại A , có AB = 6cm ;
AC 8cm , BC =10cm . Đường cao AH (H ∈ BC);
a) Chỉ ra các cặp tam giác đồng dạng ,
b) Cho AD là đường phân giác của tam giác ABC (D ∈ BC) . Tính độ dài DB và DC;
c) Chứng minh rằng AB2= BH .HC
d) Vẽ đường thẳng vuông góc với AC tại C cắt đường phân giác AD tại E. Chứng minh tam giác ABD đồng dạng tam giác ECD
Bài 15 Cho tam giác ABC vuông tại A , có AB = 3cm ; AC = 4cm. Vẽ đường cao AH (H ∈ BC)
Tính độ dài BC .
Chứng minh tam giác HBA đồng dạng với tam giác HAC
Chứng minh
Kẻ đường phân giác AD (D ∈ BC ). Tính các độ dài DB và DC ?
Bài 16: Cho tam giác ABC vuông tại A , đường cao AH. Chứng minh:
a/ AH.BC = AB.AC
b/ AB² = BH.BC
c/ AH² = BH.CH
d/ Gọi M là trung điểm của BH, N là trung điểm của AH. Chứng minh: CN AM.
Bài 17: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền thành 2 đoạn BH = 9cm và HC = 16cm. Tính AB, AC, BC.
Bài 18: Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 21cm; AC = 28cm.
a/ Tính AH
b/ Kẻ HD AB; HE AC. Tính diện tích tam giác AED.
Bài 19: Cho tam giác ABC vuông tại A có AB = 15cm, AC = 20cm. Kẻ đường cao AH, trung tuyến AM.
a/ Tính AH; BC. b/ Tính BH,CH. c/ Tính diện tích tam giác AHM.
Bài 20: Cho có ba góc nhọn, đường cao AH. Vẽ HD vuông góc AB tại D, HE vuông góc AC tại E.
a) Chứng minh: tam giác AHB đồng dạng với tam giác ADH và tam giác AHC đồng dạng với tam giác AEH.
b) Chứng minh: AD.AB = AE.AC.
c) Cho AB = 12 cm, AC = 15 cm, BC = 18 cm. Tính độ dài đường phân giác AK của (K thuộc BC)
Bài 21: Cho ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Đường phân giác góc A cắt cạnh BC tại D. Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E và BA tại K.
a/ Chứng minh ABC vuông
b/ Tính DB, DC
c/ Chứng minh tam giác EDC đồng dạng với tam giác BDK
d/ Chứng minh DE = DB
Bài 22: Cho ABC vuông tại A, cho biết AB = 15 cm, AC = 20 cm. Kẻ đường cao AH của ABC.
a) Chứng minh: tam giác AHB đồng dạng với tam giác CAB và suy ra AB² = BH.BC
b) Tính độ dài các đoạn thẳng BH và CH.
c) Kẻ HM vuông góc với AB và HN vuông góc với AC. Chứng minh: AM.AB = AN.AC
d)Chứng minh: tam giác AMN đồng dạng với tam giác ACB
Bài 23: Cho tam giác ABC vuông tại A. Đường phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC và cắt AC tại E.
a) Chứng minh tam giác DEC đồng dạng với tam giác ABC.
b) Chứng minh: DB = DE.
Bài 24: Cho tam giác ABC vuông tại A có AB = 16cm, BC = 20cm. Kẻ đường phân giác BD (D thuộc AC)
a) Tính CD và AD
b) Từ C kẻ CH vuông góc với BD tại H. Chứng minh: Tam giác ABD đồng dạng với tam giác HCD
c) Tính diện tích tam giác HCD .
Bài 25
Cho tam giác ABC có các cạnh tương ứng AB= 6cm, AC= 7cm và BC = 9cm. Tam giác A’B’C’ là một tam giác vuông tại A có A’B’= 12 cm, A’C’ = 14 cm. Hãy chứng minh hai tam giác trên đồng dạng với nhau.
Bài tập các trường hợp đồng dạng của tam giác giúp các em học sinh làm quen với các dạng bài hay gặp trong các bài thi học sinh giỏi với các câu hỏi khó giành điểm 9 – 10 và có chiến lược thời gian làm bài thi phù hợp nhất.
